线段树合集

December 12, 2020 18692

点击标题可进入题目链接

【1】入门

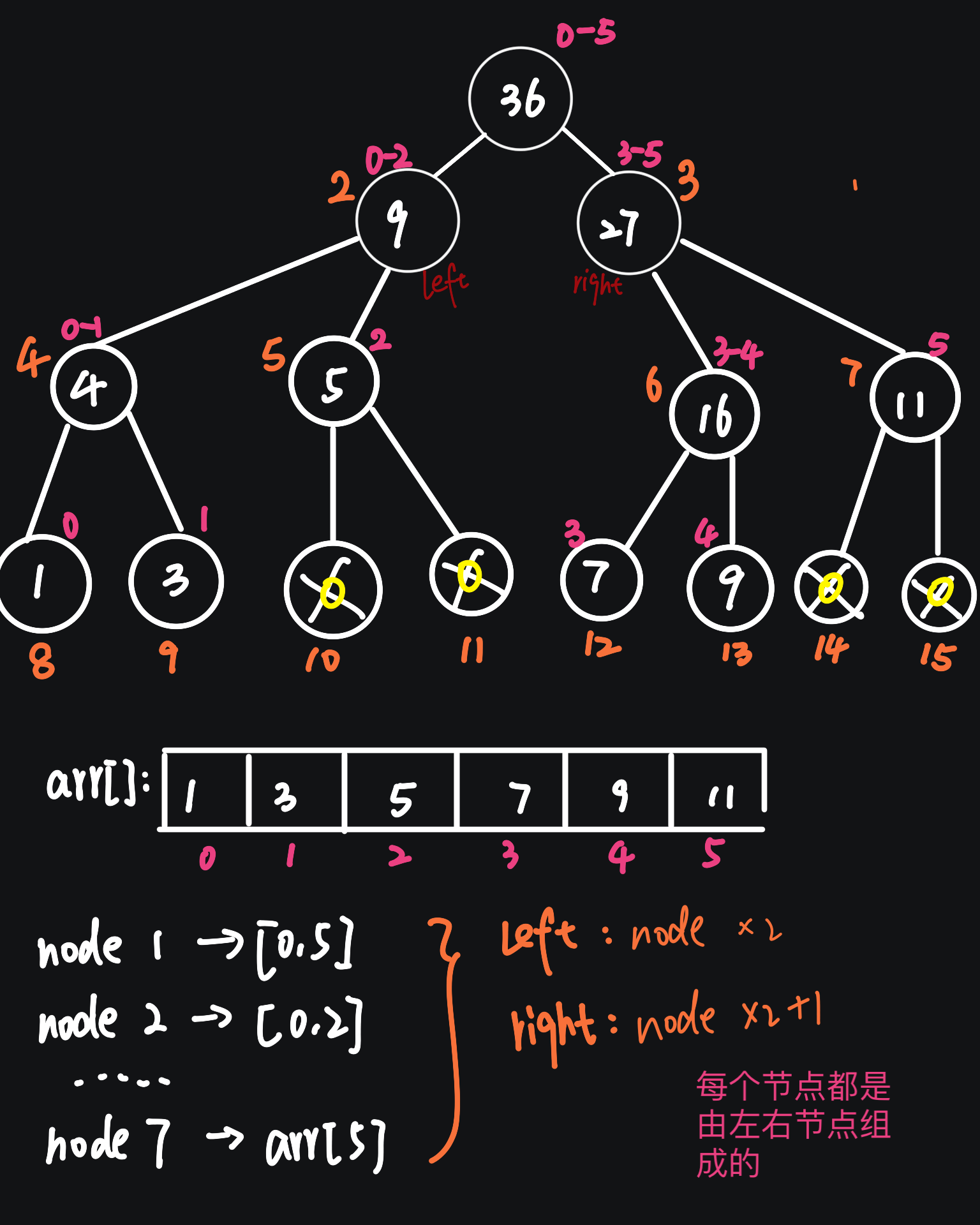
如图，一棵树由每个节点（node）组成，每个节点代表了数组[x-y]区间内的和；
每一个节点又是由子节点组成，子节点有左子节点和右子节点，如果当前节点为1，那么他的字节点为2和3，即:
节点A，左子节点为A*2，右子节点为A*2 + 1;

我们建一棵树为tree，原数组设为arr；
那么tree[node]=tree[node*2]+tree[node*2+1];（当前节点是两个子节点的和）
寻找每个节点的值，就要看子节点的值，这就用可以递归实现了。
时间复杂度为O(logn)

注意！

tree必须开4倍arr的大小，线段树是平衡二叉树，开4倍可以处理最坏情况——完美二叉树。

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[10000];
ll tree[40000];
ll n,m;
ll build_tree(ll node,ll L,ll R){//建树
    if(L==R){
        tree[node]=f[L];
    }
    else{
        ll mid=(L+R)/2;
        build_tree(node*2,L,mid);
        build_tree(node*2+1,mid+1,R);
        tree[node]=tree[node*2]+tree[node*2+1];
   }
}
ll up_tree(ll node,ll L,ll R,ll po,ll val){//修改数组arr内某个值
    if(po==L&&po==R){
        tree[node]=val;
    }
    else{
        ll mid=(L+R)/2;
        if(po>mid){
            up_tree(node*2+1,mid+1,R,po,val);
            tree[node]=tree[node*2]+tree[node*2+1];
        }
        else{
            up_tree(node*2,L,mid,po,val);
            tree[node]=tree[node*2]+tree[node*2+1];
        }
    }
}
ll get_tree(ll node,ll L,ll R,ll l,ll r){//得到数组区间l-r之内值的和
    cout<<L<<" "<<R<<endl;
    if(l>R||L>r){
        return 0;
    }
    else if(L>=l&&r>=R){
        return tree[node];
    }
    else if(L==R){
        return tree[node];
    }
    else{
        ll mid=(L+R)/2;
        ll l_sum=get_tree(node*2,L,mid,l,r);
        ll r_sum=get_tree(node*2+1,mid+1,R,l,r);
        return l_sum+r_sum;
    }
}
int main()
{
    cin>>n;
    for(ll i=0;i<n;i++){
        cin>>f[i];
    }
    build_tree(1,0,n-1);
    up_tree(1,0,n-1,4,6);//将4号点的9变为6
//    for(ll i=1;i<=15;i++){
//        cout<<"tree["<<i<<"]="<<tree[i]<<endl;
//    }
    ll ans=get_tree(1,0,n-1,2,5);/*求区间2-5的和*/
    cout<<ans<<endl;
    return 0;
}

【2】华为2016校招笔试题

思路：

就是线段树，入门是求一段区间内的总和，这次换成求max值。

注意：

  1. 本题求一段区间可能1-5，也可能5-1，所以输入后要处理一下，不然就会WA哦。
  2. 多组输入。
  3. 4倍别忘了。（由于忘记开4倍，可怜的zser又被我叨扰了）

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[30010];
ll tree[300000]; //随手开的10倍
ll n,m;
void build_tree(ll node,ll l,ll r){
    if(l==r){
        tree[node]=f[l];
    }
    else{
        ll mid=(l+r)/2;
        build_tree(node*2,l,mid);
        build_tree(node*2+1,mid+1,r);
        tree[node]=max(tree[node*2],tree[node*2+1]);
    }
}
void up_tree(ll node,ll l,ll r,ll op,ll val){
//    cout<<op<<" "<<l<<" "<<r<<endl;
    if(op==l&&op==r){
        f[op]=val;
        tree[node]=val;
    }
    else{
        ll mid=(l+r)/2;
        if(op<=mid){
            up_tree(node*2,l,mid,op,val);
        }
        else{
            up_tree(node*2+1,mid+1,r,op,val);
        }
        tree[node]=max(tree[node*2],tree[node*2+1]);
    }
}
ll get_tree(ll node,ll L,ll R,ll l,ll r){
    if(R<l||L>r){
        return 0;
    }
    else if(L==R){
        return tree[node];
    }
    else if(l<=L&&R<=r){
        return tree[node];
    }
    else{
        ll mid=(L+R)/2;
        ll l_max=get_tree(node*2,L,mid,l,r);
        ll r_max=get_tree(node*2+1,mid+1,R,l,r);
        return max(l_max,r_max);
    }
}
int main()
{
    while(scanf("%lld%lld",&n,&m)!=EOF){
    for(ll i=1;i<=n;i++){
        cin>>f[i];
    }
    build_tree(1,1,n);
    while(m--){
        getchar();
        char p;
        ll a,b;
        cin>>p>>a>>b;
        if(p=='Q'){
            ll temp;
            if(b<a){
                temp=a;
                a=b;
                b=temp;
            }

            cout<<get_tree(1,1,n,a,b)<<endl;
        }
        else{
            up_tree(1,1,n,a,b);
//            for(ll i=1;i<=15;i++){
//                cout<<"tree["<<i<<"]="<<tree[i]<<endl;
//            }
        }
    }
    }
    return 0;
}

【3】HDUoj：敌兵布阵

思路：

就是线段树，最基础的板子题。

注意：

  1. cin，cout会T！很难受！

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[50010];
ll tree[500000];
ll N,m;
void build_tree(ll node,ll l,ll r){
    if(l==r)
        tree[node]=f[l];
    else{
        ll mid=(l+r)/2;
        build_tree(node*2,l,mid);
        build_tree(node*2+1,mid+1,r);
        tree[node]=tree[node*2]+tree[node*2+1];
    }
}
void up_tree(ll node,ll l,ll r,ll op,ll val){
    if(l==r && l==op){
        f[op]+=val;
        tree[node]=f[op];
    }
    else{
        ll mid=(l+r)/2;
        if(op>mid)
            up_tree(node*2+1,mid+1,r,op,val);
        else
            up_tree(node*2,l,mid,op,val);
        tree[node]=tree[node*2]+tree[node*2+1];
    }
}
ll get_tree(ll node,ll L,ll R,ll l,ll r){
    if(l>R||L>r)
        return 0;
    else if(L>=l&&r>=R)
        return tree[node];
    else if(L==R)
        return tree[node];
    else{
        ll mid=(L+R)/2;
        return get_tree(node*2,L,mid,l,r)+get_tree(node*2+1,mid+1,R,l,r);
    }
}
int main(){
    ll T,a,b;
    cin>>T;
    ll ok=1;
    while(T--){
        printf("Case %d:\n",ok);
        ok++;
        scanf("%lld",&N);
        for(ll i=1;i<=N;i++){
                scanf("%lld",&f[i]);
        }
        build_tree(1,1,N);
        //for(ll i=1;i<=15;i++)cout<<"tree["<<i<<"]="<<tree[i]<<endl;
        char op[100];
        while(1){
        scanf("%s",op);
        if(op[0]=='E')break;
        scanf("%lld %lld",&a,&b);
        if(op[0]=='Q'){
            printf("%lld\n",get_tree(1,1,N,a,b));
             //for(ll i=1;i<=15;i++)cout<<"tree["<<i<<"]="<<tree[i]<<endl;
        }
        else if(op[0]=='A'){
            up_tree(1,1,N,a,b);
            //cout<<f[3]<<endl;
        }
        else if(op[0]=='S'){
            b=0-b;
            up_tree(1,1,N,a,b);
        }
        }
    }
    return 0;
}

【4】HDUoj：I Hate It

思路：

跟第二题除了数组大小没有任何区别了。主要用于练手，练熟线段树写法。

注意：

  1. cin，cout会T。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[200010];
ll tree[900011];
ll N,M;
void build_tree(ll node ,ll l ,ll r){
    if(l==r)
        tree[node]=f[l];
    else{
        ll mid=(l+r)/2;
        build_tree(node*2,l,mid);
        build_tree(node*2+1,mid+1,r);
        tree[node]=max(tree[node*2],tree[node*2+1]);
    }
}
void up_tree(ll node,ll l,ll r,ll po, ll val ){
    if(l==r&&po==l){
        f[l]=val;
        tree[node]=val;
    }
    else{
        ll mid=(l+r)/2;
        if(po<=mid)
            up_tree(node*2,l,mid,po,val);
        else
            up_tree(node*2+1,mid+1,r,po,val);
        tree[node]=max(tree[node*2],tree[node*2+1]);
    }
}
ll get_tree(ll node,ll L,ll R,ll l, ll r){
    if(R<l||L>r)
        return 0;
    else if(L>=l&&r>=R){
        return tree[node];
    }
    else if(L==R)
        return tree[node];
    else{
        ll mid=(L+R)/2;
        return max(get_tree(node*2,L,mid,l,r),get_tree(node*2+1,mid+1,R,l,r));
    }
}
int main(){
    while(scanf("%lld %lld",&N,&M)!=EOF){
        for(ll i=1;i<=N;i++){
            scanf("%lld",&f[i]);
        }
        build_tree(1,1,N);
        while(M--){
            getchar();
            char op;
            ll a,b;
            scanf("%c %lld %lld",&op,&a,&b);
            if(op=='Q'){
                ll temp;
                if(b<a){
                    temp=a;
                    a=b;
                    b=temp;
                }
                printf("%lld\n",get_tree(1,1,N,a,b));
            }
            else{
                up_tree(1,1,N,a,b);
            }
        }
    }
    return 0;
}

【5】进阶:延迟标记——区间修改

1.理解懒标

延迟标记——懒标，用于解决区间修改，入门是更新某一个点，而懒标可以实现区间更新，比如要求区间[a,b]之间所有值加一，用懒标标记可以大大减少时间复杂度。
现在我们的树用结构体来建：

1
2
3
4
struct trees{
    ll l,r,sum;
    ll lazy;//懒标
}tree[40000];

（当然也可以开数组，看个人习惯叭，不开结构体只需要两个数组，一个lazy数组，一个tree数组，我感觉是比结构体更节省空间的。不知道单开数组和递归传递数哪个更耗空间。）

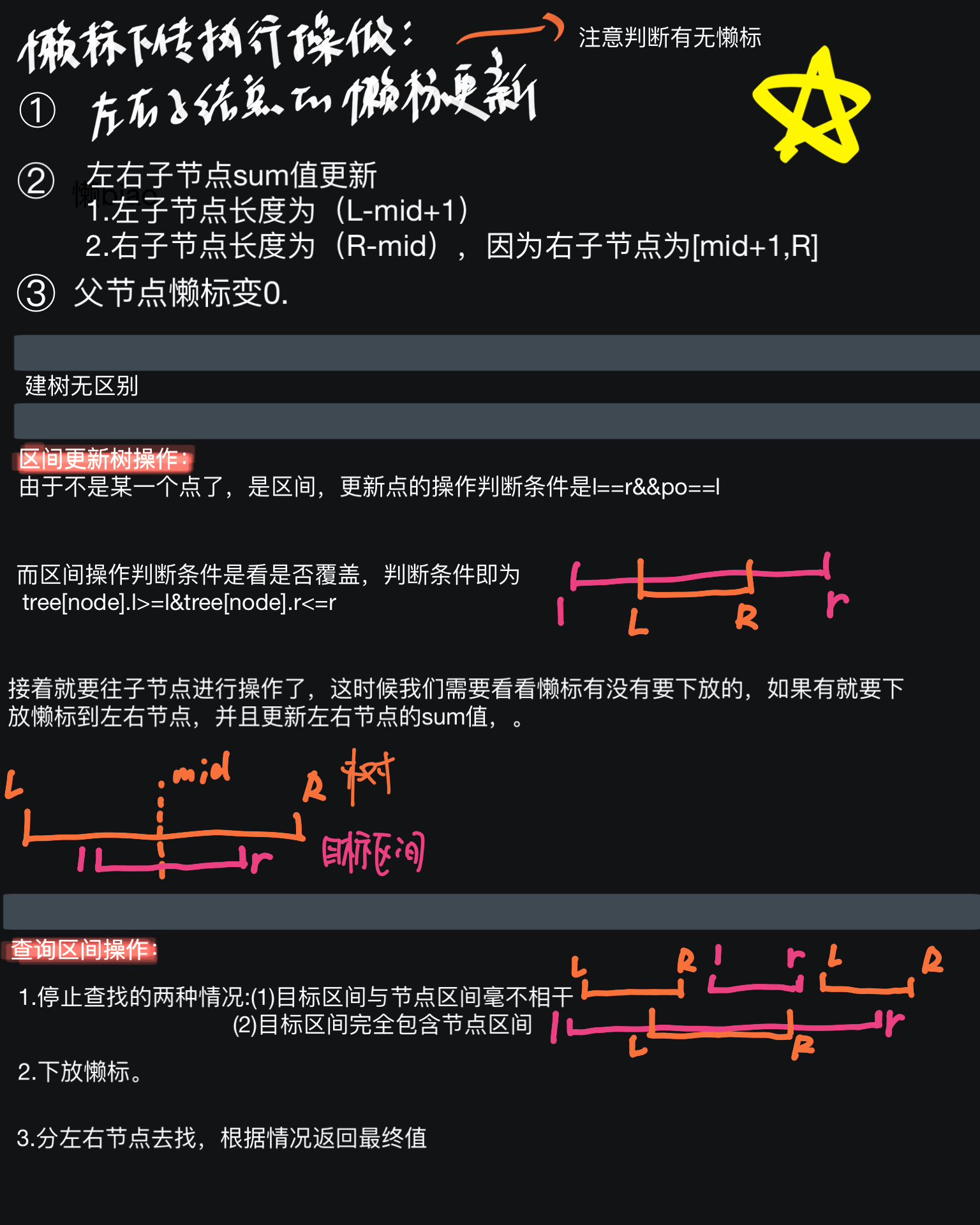
2.懒标下放

懒标下放是最重要的，但是也很好理解，就是在需要的时候，把本来应该传下去，但是偷懒没有传下去的值传下去，当然，只有在查询和修改线段树时懒标才会用下放，因为建树根本没用上。
代码很好理解，只有三步（如果这里看不懂，总结里写了三步具体是什么）：

1
2
3
4
5
6
7
8
9
10
11
12
13
//懒标下放
ll pushdown(ll node){
    if(tree[node].lazy!=0){
        tree[node*2].lazy+=tree[node].lazy;
        tree[node*2+1].lazy+=tree[node].lazy;

        ll mid=(tree[node].l+tree[node].r)/2;
        tree[node*2].sum+=((mid-tree[node].l+1)*tree[node].lazy);
        tree[node*2+1].sum+=((tree[node].r-mid)*tree[node].lazy);

        tree[node].lazy=0;
    }
}

3.总结

参上拙略总结：


代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[10000];
ll lazy[40000];
struct node{
    ll l,r,sum;
    ll lazy;
}tree[40000];
ll n,m;
ll pushdown(ll node){
    if(tree[node].lazy!=0){
        tree[node*2].lazy+=tree[node].lazy;
        tree[node*2+1].lazy+=tree[node].lazy;
        ll mid=(tree[node].l+tree[node].r)/2;
        tree[node*2].sum+=((mid-tree[node].l+1)*tree[node].lazy);
        tree[node*2+1].sum+=((tree[node].r-mid)*tree[node].lazy);
        tree[node].lazy=0;
    }
}
ll build_tree(ll node,ll l ,ll r){
    tree[node].l=l;
    tree[node].r=r;
    if(l==r)
        tree[node].sum=f[l];
    else{
        ll mid=(l+r)/2;
        build_tree(node*2,l,mid);
        build_tree(node*2+1,mid+1,r);
        tree[node].sum=tree[node*2+1].sum+tree[node*2].sum;
    }
}
ll up_tree(ll node,ll l,ll r ,ll val){
    if(tree[node].l>=l&&tree[node].r<=r){//完全覆盖
        tree[node].sum+=(tree[node].r-tree[node].l+1)*val;//修改该段值
        tree[node].lazy+=val;//下面的节点本来也该变，但是我们懒得跑了，于是存放起来
    }
    else{
        pushdown(node);
        ll mid=(tree[node].l+tree[node].r)/2;
        if(l<=mid)up_tree(node*2,l,r,val);
        if(r>mid)up_tree(node*2+1,l,r,val);
        tree[node].sum=tree[node*2].sum+tree[node*2+1].sum;
    }
}
ll get_tree(ll node,ll l,ll r ){
    if(tree[node].r<l||tree[node].l>r)
        return 0;
    if(tree[node].l>=l&&tree[node].r<=r)
        return tree[node].sum;
    ll mid=(tree[node].l+tree[node].r)/2;
    ll s=0;
    if(l<=mid)s+=get_tree(node*2,l,r);
    if(r>mid)s+=get_tree(node*2+1,l,r);
    return s;

}
int main()
{
    cin>>n;
    for(ll i=1;i<=n;i++){
        cin>>f[i];
    }
    build_tree(1,1,n);
    for(ll i=1;i<=7;i++){
        cout<<"tree["<<i<<"]="<<tree[i].sum<<endl;
        cout<<"tree["<<i<<"].lazy="<<tree[i].lazy<<endl;
    }
    cout<<endl<<endl<<endl;
    up_tree(1,1,3,1);//1-3都+1
    for(ll i=1;i<=15;i++){
        cout<<"tree["<<i<<"]="<<tree[i].sum<<endl;
        cout<<"tree["<<i<<"].lazy="<<tree[i].lazy<<endl;
    }
    ll ans=get_tree(1,2,4);//求区间2-5的和
    cout<<ans<<endl;
    return 0;
}

【6】HDUoj：Just a Hook

思路：

区间修改，这个的话很容易发现，懒标不需要相加，是直接替换，所以在基础上改一改就能AC了。

注意：

结构体初始化。

一点搞笑题外话：写这个题的时候没注意自己开的中文翻译模式，然后直接复制的中文输出去提交，WA了，给我整蒙了还哈哈哈，结果才发现输出应该是英文。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include  "stdio.h"
#include  "iostream"
#include <string.h>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[100010];
struct trees{
    ll l,r,sum;
    ll lazy;
}tree[400000];
ll n,m;
ll T;
ll pushdown(ll node){
    if(tree[node].lazy!=0){
        tree[node*2].lazy=tree[node].lazy;
        tree[node*2+1].lazy=tree[node].lazy;
        ll mid=(tree[node].l+tree[node].r)/2;
        tree[node*2].sum=((mid-tree[node].l+1)*tree[node].lazy);
        tree[node*2+1].sum=((tree[node].r-mid)*tree[node].lazy);
        tree[node].lazy=0;
    }
}
void build_tree(ll node,ll l ,ll r){
    tree[node].l=l;
    tree[node].r=r;
    if(l==r){
        f[l]=1;
        tree[node].sum=1;
    }
    else{
        ll mid=(l+r)/2;
        build_tree(node*2,l,mid);
        build_tree(node*2+1,mid+1,r);
    }
}
void up_tree(ll node,ll l,ll r,ll val){
    if(tree[node].l>=l&&tree[node].r<=r){
            tree[node].sum=((tree[node].r-tree[node].l+1)*val);
            tree[node].lazy=val;
    }
    else{
        pushdown(node);
        ll mid=(tree[node].l+tree[node].r)/2;
        if(l<=mid)
            up_tree(node*2,l,r,val);
        if(r>mid)
            up_tree(node*2+1,l,r,val);
        tree[node].sum=tree[node*2].sum+tree[node*2+1].sum;
    }

}
ll get_tree(ll node,ll l,ll r){
    if(tree[node].l>=l&&tree[node].r<=r)
        return tree[node].sum;
    else if(tree[node].l==tree[node].r)
        return tree[node].sum;
    else if(tree[node].r<l||tree[node].r>r)
        return 0;
    else {
        pushdown(node);
        ll mid=(tree[node].l+tree[node].r)/2;
        ll s=0;
        if(l<=mid)
            s+=get_tree(node*2,l,r);
        if(r>mid)
            s+=get_tree(node*2+1,l,r);
        return s;

    }
}
int main()
{
    scanf("%lld",&T);
    ll ok=1;
    while(T--){
        memset(tree,0,sizeof(struct trees)*40000);
//        cout<<"查看初始化："<<endl;
//        for(ll i=1;i<=2*n+1;i++){
//            cout<<"tree["<<i<<"]="<<tree[i].sum<<endl;
//        }
        scanf("%lld%lld",&n,&m);
        build_tree(1,1,n);
        ll a,b,c;
        for(ll i=1;i<=m;i++){
            scanf("%lld%lld%lld",&a,&b,&c);
            up_tree(1,a,b,c);
        }
//        for(ll i=1;i<=2*n+1;i++){
//            cout<<"tree["<<i<<"]="<<tree[i].sum<<endl;
//        }
        printf("Case %lld: The total value of the hook is %lld.\n",ok++,get_tree(1,1,n));
    }
    return 0;
}

【7】HDUoj：Atlantis

缠了我差不多一个月，我是笨比！！！

离散化+扫描线+线段树

题意：

给定方块的左下角和右上角，形成一个方块，有很多不同的方块，求最后形成的图形的总面积。（如图所示）


思路：

定义线段树来维护底边长和覆盖边数:

  1. len：底边长
  2. vis：覆盖边数

扫描线有l,r,h,vis属性：

  1. l,r：区间
  2. h：高（两条扫描线的高度差就是当前面积的高了）
  3. vis：定义当前扫描线是图形的底边还是顶边。

图形最终就是由扫描线扫过的小面积，底边*高，最后每个扫过的图形面积相加。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <iostream>
#include <algorithm>
#include <cstring>
#include <stdio.h>
using namespace std;

const int maxn=2e4+5;

struct line
{
    double l,r,h;
    int vis;
    bool operator<(const line &t) const
    {
        return h<t.h;
    }
}e[maxn];

struct tree
{
    int vis;
    double len;
}tr[maxn*8];

int n,cnt;
double x[maxn];
double a,b,c,d;

void pushdown(int p,int l,int r)
{
    cout<<"L="<<l<<" R="<<r<<endl;
    cout<<"tree["<<p<<"]="<<tr[p].vis<<" "<<tr[p].len<<endl;
    if(tr[p].vis) tr[p].len=x[r+1]-x[l];//因为这里线段树维护的是一个个的区间[L,L+1]，所以r+1
    else if(l==r) tr[p].len=0;
    else tr[p].len=tr[p<<1].len+tr[p<<1|1].len;
}

void update(int p,int l,int r,int L,int R,int v)//当前根节点p，用来更新的区间[l,r],当前更新区间[L,R],当前线段的标记量v：vis
{
    if(L>=l&&R<=r){
        tr[p].vis+=v;
        pushdown(p,L,R);
        return;
    }
    int mid=L+R>>1;
    if(l<=mid) update(p<<1,l,r,L,mid,v);
    if(r>mid) update(p<<1|1,l,r,mid+1,R,v);
    pushdown(p,L,R);
}

int main()
{
    int t=0;
    while(cin>>n,n){
        memset(tr,0,sizeof tr);
        cnt=0;
        for(int i=0;i<n;i++){
            cin>>a>>b>>c>>d;
            x[cnt]=a;
            e[cnt++]={a,c,b,1};
            x[cnt]=c;
            e[cnt++]={a,c,d,-1};
        }
        //对底边进行离散化：
        sort(x,x+cnt);
        int xs=unique(x,x+cnt)-x;
        //对底边按高排序：
        sort(e,e+cnt);
        double res=0;
        //扫描线从x轴往外依次扫描：
        for(int i=0;i<cnt;i++){
            //当前底边长[pl,pr]
            int pl=lower_bound(x,x+xs,e[i].l)-x;
            int pr=lower_bound(x,x+xs,e[i].r)-x-1;//因为一个结点维护的是一个区间，所以区间序号为L，R为区间序号+1
            update(1,pl,pr,0,xs,e[i].vis);
            res+=tr[1].len*(e[i+1].h-e[i].h);//当前矩形面积=(当前矩形底边长：线段树维护的当前覆盖在x轴上的总长度)*(当前矩形高度：e[i+1].h-e[i].h)
        }
        cout<<"lines"<<endl;
        for(int i=0;i<cnt;i++)
            cout<<"line["<<i<<"]="<<e[i].l<<" "<<e[i].r<<" "<<e[i].h<<endl;
        printf("Test case #%d\n",++t);
        printf("Total explored area: %.2f\n",res);
        cout<<endl;
        
    }
    return 0;
}

  • 本文作者：lybbor
  • 版权声明：本博客所有文章均采用 BY-NC-SA 许可协议，转载请注明出处！