欧拉筛

April 12, 2021 1510

普通暴力素数筛

1
2
3
4
5
6
7
8
9
10
static final int N = 1e7 + 5;
int st[N]; // 初始化为0， 0表示质数，1表示合数
for(int i = 2; i <= n; i++){
	for(int j = 2; j <= i / j; j++){//试除法
		if(i % j == 0){
			st[i] = 1; // 合数，标记为1 
		}
	}
}

时间复杂度O(n)

进阶筛的数学原理

  1. 一个合数一定能被分解为几个质数的幂的乘积
  2. 这个数的质因子一定是小于它本身

埃氏筛法

1
2
3
4
5
6
7
8
9
10
static final int N = 1e7 + 5;
static int[] st = new int[N];
public static void E_sieve(int  n){
	for(int i = 2; i <= n; i++){
		if(st[i] == 0){
			for(int j = 2 * i; j <= n; j += i)
			    st[j] = 1; // j是i的一个倍数，j是合数，筛掉。
		}
	}
}

时间复杂度为：O(nloglog2n)

埃氏筛有什么可以优化的地方？

  1. 重复筛了
    比如6，被2筛了，被3筛了
  2. 最小质因子一定小于根号n
    所以直接从2-根号n

优化的埃氏筛

1
2
3
4
5
6
7
8
9
10
11
12
static final int N = 1e7 + 5;
static int[] st = new int[N];
public static void E_sieve(int  n){
	for(int i = 2; i <= n / i; i++)
	{
		if(st[i] == 0)
		{
			for(int j = i * i; j <= n; j += i)
			    st[j] = 1; // j是i的一个倍数，j是合数，筛掉。
		}
	}
}

优化后近似O(n)了。

欧拉筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
static final int N = 1e7 + 5;
static int[] st = new int[N], primes = new int[N];
void ola(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i] == 0) primes[cnt ++ ] = i;//将质数存到primes中
        for (int j = 0; primes[j] <= n / i; j ++ )//要确保质数的第i倍是小于等于n的。
        {
            st[primes[j] * i] = 1;
            if (i % primes[j] == 0) break;
        }
    }
}

时间复杂度O(n)

核心点解析

i%prime[j]==0

当i=k*prime[j]时
如果继续j+1:
i*prime[j+1]=k*prime[j]*prime[j+1]
这个时候的素数已经是之前被标记过的了
所以i%prime[j]==0时就退出，避免二次标记

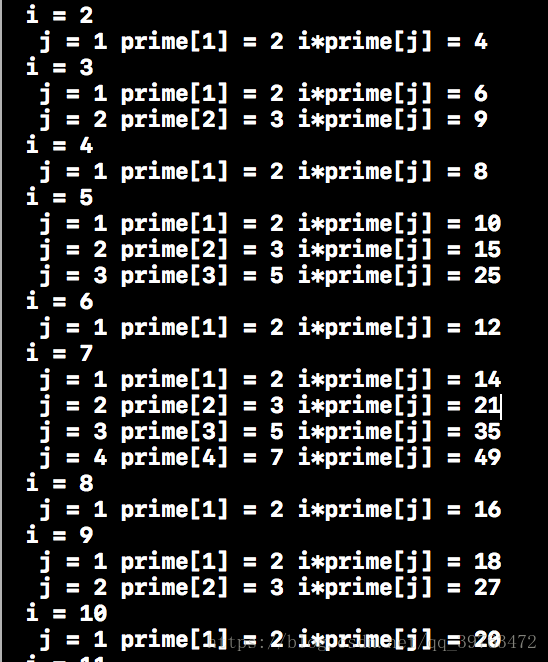
看输出就懂了：
欧拉筛输出

  • 本文作者：lybbor
  • 版权声明：本博客所有文章均采用 BY-NC-SA 许可协议，转载请注明出处！