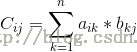前缀和、差分约束、快速幂、矩阵快速幂

April 23, 2021 3068

一、前缀和

m次求一段区间内的和，要求时间复杂度为O(m)
是不是区间一下想到了线段树，但是线段树的话，时间复杂度是O(mlogn)，要被卡。

下标 0 1 2 3 4 5
nums 0 2 3 1 5 6
pre 0 2 5 6 11 17

由图可得：
求[1,2]区间所有值的和为：pre[2]-pre[2-1]=5-0=5
求[3,5]区间所有值的和为：pre[5]-pre[3-1]=17-5=12

所以：求[x,y]区间内所有值的和公式为：pre[y]-pre[x-1]

二、差分约束

m次区间修改（这回一下想到的是线段树的懒标下放），要求时间复杂度为O(m)。
如果线段树，还是O(mlogn)，不可。

预处理

下标 0 1 2 3 4 5 6
nums 0 2 3 5 7 2 4
D 0 2 1 2 2 -5 2

不难看出D数组是每当前nums和上一位nums的差值
nums[5]=D[1]+D[2]+D[3]+D[4]+D[5]=2
所以nums[i]=D[1]+….+D[i-1]+D[i];

我们以这样的方式来把D数组建立出来。

区间操作

修改[2,5]区间，区间内每位数加上5
那么我们的区间其实只需要修改D[2]和D[5+1]

下标 0 1 2 3 4 5 6
nums 0 2 8 10 12 7 4
D 0 2 6 2 2 -5 -3

将原来的D[2]+5，原来的D[5+1]-5；
所以[x,y]区间内每个数加上A的话：

D[x]+=A;D[y+1]-=A;

三、快速幂（重点）

我觉得很无敌哈，很天才，其实就是二分的思想。
用于解决(a^b)%c

有pow()函数，快速幂的意义？

之前太愚蠢了，我觉得有pow了，为什么还要手写快速幂，后来看了pow函数才知道：
pow函数返回的是double类型
而且在解决有模运算的情况会出大问题，比如2的1000000000次方取模1e7，那么那个2的1000000000次方用什么来存放呢？？

取模运算的性质

(a * b )%p=( a%p * b%p )%p

设a = p*k1 + q1;
b = p*k2 + q2;

( a * b )
=(p*k1 + q1)*(p*k2 + q2)
=(p*k1 * p*k2)+(p*k1 * q2)+(p*k2 * q1)+q1*q2

(a * b )%p=[(p*k1 * p*k2)+(p*k1 * q2)+(p*k2 * q1)+q1*q2]%p
=(q1 * q2)%p

(a%p * b%p)= q1*q2

∴ (a * b )%p=( a%p * b%p )%p

由推导可知，a^b是每次将指数b除以2
当指数为奇数的时候

ans=ans*a
a=a*a
b/=2

指数为偶数时

a=a*a
b/=2

加上取模操作的话
当指数为奇数的时候

ans=((ans%c)*(a%c))%c
a=((a%c)*(a%c))%c
b/=2

指数为偶数时

a=(a*a)%c
b/=2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ll fast_(ll a,ll b ,ll c){
    ll ans=1;
    while(b){
        if(b&1){
            ans=(ans*a)%c;
        }
        a=(a*a)%c;
        b>>=1;
    }
    return ans;
}
int main(){
    ll a,b,c;
    while(1){
    cout<<"请输入a,b,c："<<endl;
    cin>>a>>b>>c;
    cout<<"ans="<<fast_(a,b,c)<<endl<<endl;
    }
    return 0;
}

例题 Leetcode 50.Pow(x, n)

点击进入题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    double myPow(double x, int n) {
        int tmp=abs(n);
        double ans=1.00;
        while(tmp){
            if(tmp&1){
                ans=ans*x;
            }
            x=x*x;
            tmp=tmp/2;
        }
        if(n<0){
            return 1/ans;
        }
        return ans;
    }
};

四、矩阵快速幂

计算矩阵M^b %C
M^5 =M^2 * M^2 * M;
由矩阵的性质：

矩阵计算

所以由矩阵的性质，我们可以得出，只需要重载一下快速幂中的乘法，就可以实现矩阵快速幂了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
typedef long long ll;
const int mod = 1e9 + 7;
const int MAXN = 10005;//矩阵的大小
struct Mat {
    ll m[MAXN][MAXN];
}ans, a;//ans为结果矩阵，a为输入矩阵
Mat Mul(Mat a, Mat b, int n) {//计算矩阵a乘矩阵b，n为矩阵的大小
    Mat c;//临时矩阵c
    memset(c.m, 0, sizeof(c.m));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                c.m[i][j] = (c.m[i][j] + (a.m[i][k] * b.m[k][j]) % mod) % mod;
    return c;
}
Mat _power(Mat a, int b, int n) {//计算a^b，n为矩阵的大小
    for (int i = 1; i <= n; i++)//构造单位矩阵
        ans[i][i] = 1;
    while (b) {
        if (b & 1)
            ans = Mul(ans, a, n);
        a = Mul(a, a, n);
        b >>= 1;
    }
    return ans;
}
  • 本文作者：lybbor
  • 版权声明：本博客所有文章均采用 BY-NC-SA 许可协议，转载请注明出处！